INSULATORS Groundbreaking discovery of Topological Insulators

Related Vendors

CeramTec GmbH

ROHM Semiconductor GmbH

Rogers Corporation

A topological insulator looks like an insulator from the inside but actually functions like a conductor. You can think of a combo of an insulator and a conductor. Surprisingly, topological insulators are compared to the analogy of donuts being similar to a coffee cup! But isn’t such a device weirdly impossible to exist? Well, topological insulators made their inventors win the 2016 Nobel Prize in Physics. They even have their own periodic table!

Topological insulators are quantum materials that are internally insulators in the bulk but externally electrical conductors across the surface/edges. Simply put, topological insulators are characterized by an insulating bulk interior and a conducting surface. Topological insulators are named such because they exhibit a property known as topology.

Topological Insulators: Why are they so unique?

The nontrivial topology of wave functions and time reversal symmetry of the surface states make them what they are— topological insulators. Such properties prevent failure under deformation or any non-magnetic structural disorder. The electrons in the conductive surface of topological insulators become insensitive to physical defects.

Quantum behavior

Topological insulators are quantum materials. It is a well-known fact that water freezes into ice at a lower temperature due to thermal effects. At temperatures near absolute zero (-273.15 degrees Celsius), particles begin to form quantum vortices. They are tiny spinning whirlpool patterns of current.

When the temperature rises slightly, bound vortices unbind. The process is a quantum phase transition. The maximum temperature at which vortices unbind is called the KT (Kosterlitz-Thouless) temperature. It is still a low temperature, slightly above absolute zero. Vortices unbind not due to a symmetrical change but because of topological behavior.

QUANTUM TECHNOLOGY

Nanomaterials under tension: Advancing quantum technology innovations

Energy bands

In insulators, energy bands are separated over large distances, up to 6 eV. In conductors, energy bands overlap. On the other hand, a small separation exists between energy bands of semiconductors, up to 3-4 eV. In topological insulators, the bulk energy band gap is similar to that of semiconductors.

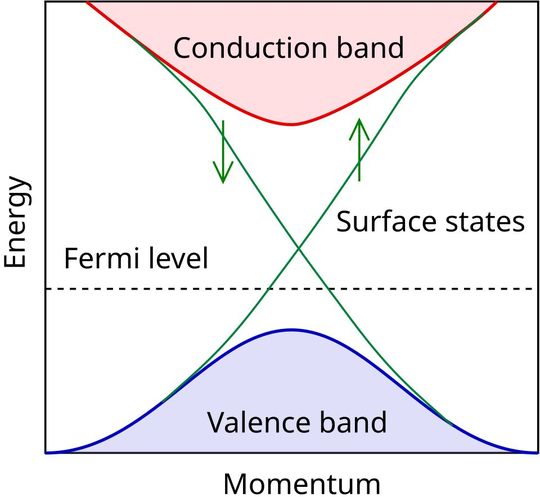
The blue-colored valence band shows the low-energy region where electrons reside. The pink-colored region depicts the empty conduction band. The dotted line shows the Fermi level. Electrons do not exist above the Fermi level. It is like an energy border. Any insulator can only conduct through its surface states. Electrons can be excited through a large voltage or heat to leave the valence band and enter the conduction band.

Topological insulators exhibit a band inversion property. In general, the energy of the valence band is lower than the energy of the conduction band. Due to spin-orbit interactions, the energy of the conduction band drops lower than the valence band at certain points. Such a property is called band inversion. The presence of band inversion results in nontrivial topology of wavefunctions and special surface states to form a Dirac cone.

Dirac cone

Green lines that form an V-shaped structure represent the Dirac cone. The Dirac cone is a V-shaped structure that sits inside the bulk band gap of topological insulators. It is centered on the Fermi level. The tip of the Dirac cone is called the Dirac point. At this point, the valence band and conduction bands meet linearly. The energy of electrons changes linearly with momentum.

In the Dirac cone, electrons behave as relativistic massless Dirac particles. They move fast, with very little resistance. However, the Dirac cone extends only up to the surface of the material. It does not exist over the bulk interior. As a result, topological insulators are conductors through the surface and insulators inside.

Topological property

The inventors discovered a new type of quantum transition occurring in ultra-thin 2D layers because of topology. Topology is a branch of mathematics that deals with properties that cannot change under the subject of deformations, such as stretching, bending, or compressing. The presence of topological properties is due to spin-orbit coupling. It is the same quantum phase transition we talked of and time-reversal symmetry.

The inventors built their foundation of topological insulators on the quantum Hall effect (1980s) observed in 2D sheets under strong magnetic fields. Topological insulators do not need a magnetic field for such behavior. As mentioned above, the inventors list the example of a donut and a coffee cup being of the same topology due to the presence of a hole.

As mentioned above, the wavefunctions exhibit a nontrivial topology. Topological invariant, denoted by "Z", is a mathematical concept that facilitates bulk conduction between the energy band surfaces in a topological insulator. It protects the surface conductive states. In simple words, topology is the main property of topological insulators that preserves their characteristics under deformation.

Summing up: Cool facts of topological insulators

Topological insulators are quantum materials with an unusual combination of properties—insulating in the bulk while supporting robust conduction at their edges or surfaces.

Insensitive to deformation: Topological insulators cannot change their operation or fail when they are deformed, stretched, or bent. They can never be torn apart. However, a “magnetic event” can induce failure modes.

Types: Topological insulators are of two types: 2D and 3D.

Similarity with superconductors: Most topological insulators exist at low temperatures near absolute zero. Some high-temperature topological insulators exist as well.

Periodic table: Just like the chemistry periodic table, topological insulators, along with superconductors, form a separate periodic table.

SUPERCONDUCTING BEHAVIOR

MIT physicists observe key evidence of unconventional superconductivity in graphene

How can topological insulators be useful?

Bismuth selenide, bismuth telluride, antimony telluride, and mercury telluride are some examples of topological insulators. Let us look at how they can be effective in various applications.

Quantum computing

As mentioned above, topological insulators consist of quantum vortices. Topological insulators sometimes contain Majorana fermions, a type of particle which is its own antiparticle. So, they contain a pair of vortices and anti-vortices that could result in quantum entanglement and superposition. As a result, topological insulators can be applicable in fault-tolerant, robust quantum computers.

Topological transistor

Topological materials can be both insulators and conductors. It means topological insulators, topological conductors, topological semiconductors, topological semimetals, and topological superconductors exist. Topological transistors may operate at half the voltage and consume one quarter of the energy consumed by conventional silicon-based transistors. They can solve heavier energy usage and slower switching patterns in the semiconductor industry.

Topological semimetals

Topological semimetals are one of the best electrical conductors with minimal energy loss. They remain insensitive to temperature and chemical variations. There are three types of topological semimetals: Dirac, Weyl, and Nodal-line. The valence band and conduction band touch at one point in Dirac semimetals, two points in Weyl semimetals, and along a loop in nodal-line semimetals.

POWER EFFICIENCY

Quantum dot lasers could redefine power system performance

Fastest transistor

China has recently invented one of the fastest transistors in the world. It is none other than bismuth selenide, a topological material. The topological insulator-transistor is expected to compute faster than traditional transistors. Surface currents are dissipationless, making them ultra-low energy devices that solve heat management problems in power electronics.

Power control

Some topological insulators are capable of remaining stable at room temperature. They can function as excellent sensors and controllers to power remote areas and even industrial systems. Isolation in power electronics is a crucial part of safe operations. Magnetoelectric power control systems can use topological insulators to offer no-contact power control in high-voltage and high-current systems.

Optoelectronics

Topological insulators are used in photodetectors and some advanced optoelectronic devices. They are known to improve overall laser performance, imaging functionalities in medical scans, infrared sensing capabilities, and free-space beyond 5G or 6G communication systems. Topological Weyl semimetals such as tantalum arsenide are known to convert infrared light to electricity and recycle heat.

Thermoelectrics

Thermoelectric materials convert heat into electricity. For efficient heat-to-electricity conversion, thermoelectric materials must exhibit low thermal conductivity, high electrical conductivity, and high seed back coefficient. Band inversion properties of topological insulators reduce thermal conductivity and boost the seed back coefficient. As a result, a healthy balance of electric conductivity, thermal conductivity, and seed back coefficient exists.

Spintronics

Spintronics is defined as the method of storing, transferring, and processing information through the spin of electrons. Conventional spintronic applications use magnetic materials to control spin. Topological insulators, being quantum materials, are a good candidate for spintronic applications. They can undergo spin-momentum locking to yield higher efficiency at low power. Possible applications could be spin diodes and spin transistors.